历史上一共有三次工业革命:
18世纪60年代,第一次工业革命从英国发起,以大规模工厂化生产取代个体工场手工生产的一场生产与科技革命。
19世纪中期,第二次工业革命是指电力取代蒸汽动力的新能源。电力工业和电器制造业迅速发展起来。此时,人类跨入了电气时代。
20世纪后半期,第三次科技革命以原子能、电子计算机、空间技术和生物工程的发明和应用为主要标志。人类进入了信息时代。
信息时代的最大特征是不确定性,而信息论就是人类对抗不确定性,最重要和有效的方法论。
信息度量
对于一条信息,重要的是找出其中有多少信息量,要搞清楚“信息量”,就要对信息进行量化的度量。但人们始终没找到量化度量信息的桥梁,也就是缺少一个合适的“衡量单位”,比如你用天平称重,需要在另一边摆放相应重量的砝码,那衡量信息的砝码是什么呢?
香农最大的贡献在于找到了这个“砝码”,也就是将信息的量化度量和不确定性联系起来。他给出一个度量信息量的基本单位-“比特”。
我们把充满不确定性事件的黑盒子就叫做“信息源”,它里面的不确定性叫做“信息熵”,而“信息”就是用来消除这些不确定性的信息熵,所以搞清楚黑盒子里是怎么一回事,需要的“信息量”就等于黑盒子里的“信息熵”
一个系统中的状态数量,也就是可能性,越多,不确定性就越大;在状态数量保持不变时,如果各个状态的可能性相同,不确定性就很大;相反,如果个别状态容易发生,大部分状态都不可能发生,不确定性就小。
香农把这个原理用公式表示出来了,从此信息不仅可以度量了,信息熵也可以计算了。
信息熵的定义:
\[H(X)=-\sum_{x \in \chi} p(x) \log _{2}p(x)\]其中$X$为随机变量,$X$的样本空间为$\chi$,$p(x)$是输出$x$的概率。
log以2为底可以算出同等概率下最优的尝试次数,和二分查找时间复杂度为$\log_{2}(n)$原理类似。
仔细看信息熵的公式,其中对概率取负对数表示了一种可能事件发生时候携带出的信息量。把各种可能表示出的信息量乘以其发生的概率之后求和,就表示了整个系统所有信息量的一种期望值。从这个角度来说信息熵还可以作为一个系统复杂程度的度量,如果系统越复杂,出现不同情况的种类越多,那么他的信息熵是比较大的。如果一个系统越简单,出现情况种类很少(极端情况为 1种情况,那么对应概率为 1,那么对应的信息熵为 0),此时的信息熵较小。
举个例子,当随机变量只取两个值,例如 1,0 时,即 X 的分布为:
\[P(X=1)=p, \quad P(X=0)=1-p, \quad 0 \leq p \leq 1\]熵为:
\[H(p)=-p \log _{2} p-(1-p) \log _{2}(1-p)\]这时,熵(y轴)随概率(x轴)变化的曲线如下图所示(单位为比特):
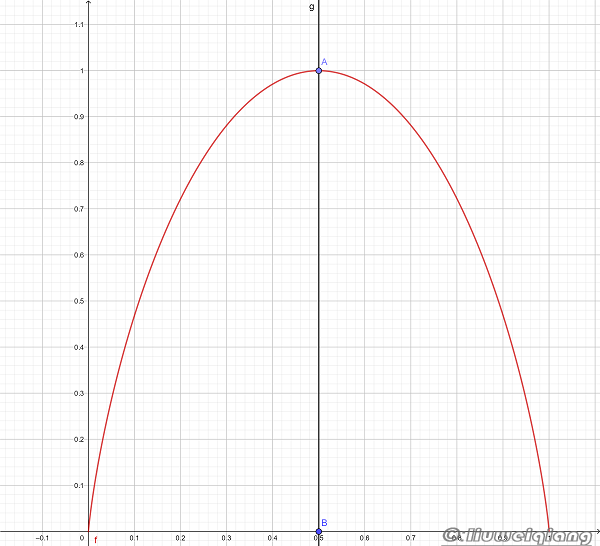
当 $p = 0$ 或 $p = 1$时, $H ( p ) = 0$,随机变量完全没有不确定性。
当 $p = 0.5$ 时,$H ( p ) = 1$, 熵取值最大,随机变量不确定性最大。
因此永远不要听那些正确率总是50%的专家的建议,因为那相当于什么都没说,没有提供能够减少“信息熵”的“信息量。
信息编码
早期人类对信息的编码,基本上是每一种信息,都有一种相应的编码。要想表达5这个数字,就伸五个指头,但是很快人的十个指头就不够用了,于是早期不少文明就把脚给用上了。
再后来,手脚并用也不够了,于是人类就在石头和骨头上划道道。再往后,当数字多到划道道也无法表达时,就有了对数字的编码,也就是各种文明的数字(用有限数字的组合可以表示更多的数)。
我们如果要表达100个数字,
第一种是设计100个不同的编号,让它们一对一对应,
另一种是只设计几种编号,然后相互组合,来表达100个数。
虽然第二种方法更简洁,但这两种方法,在信息论中是等价的。
第一种:
用100种符号对应这100个数字,这种编码所能表示的信息量,其实就是100选一的问题,也就是$\log_{2}{100}=6.65$比特。由于一个编码正好表示一个数,因此编码的长度为一。
第二种:
采用十进制编码,也就是用10种符号,每个符号所代表的信息量只有$\log_{2}{10}=3.325$比特,但是10个符号想表示100个数字,就需要两两组合。也就是说,一个符号无法消除100个数中的不确定性,这样两个符号的信息量加起来还是6.65比特,正好可以消除100个数的不确定性。
当然,我们还可以用二进制编码,就是只有0和1这两个符号,它们所包含的信息只有$\log_{2}=1$比特,如果我们想用它们来表达100个数,则需要6.65个码。进位取整以后,也就是7位的码长,才能表示100个数字。
符号越少,意味着码位越长,所以二进制通常是一长串的0101……由此可见,对数字的各种编码其实是等价的,无非是平衡编码复杂性和编码长度之间的关系
香农第一定律
也叫做无失真信源编码定理。
考虑序列发送系统,其中的序列都是来自于$X$的 $n$个字符。如果序列中的每一个字符都服从$p(x)$分布,也就是说,它们独立同分布。
那么: \(H(X) \leq L_{n}<H(X)+\frac{1}{n}\) 其中 $L_{n}$为每输入字符期望码字长度,因此,通过使用足够大的分组长度(在该文通俗理解为编号),可以获得一个编码,可以使其每字符期望码长任意地接近熵。
通俗的说:任何编码的长度都不会小于信息熵,也就是通常会大于等于信息熵,当然最理想的就是能等于。如果编码长度太短,小于信息熵,就会出现损失信息的现象。
用上面的例子作个解释:
需要表示100个数,因此n等于100,而$H(X)$此时等于6.65比特,因此要想不失真的编码信息:
\[6.65\leq L_{n}<6.66\]假如用10进制来编码100个数,那每个码字长度是3.325比特,那就需要两个码字,因此编码的长度就需要上面的$L_{n}$除以每个码字的信息量,
进而可以推出下面的结论:
编码长度 ≥ 信息熵(信息量)/ 每一个码的信息量
由于这个公式给出了$L_{n}$的下界,明确了期望码字的最小比特长度,因此它定义了在无损情况下,数据压缩的临界值。
在无损压缩的情况下,压缩任何东西所需要的比特数都大于香农第一定理所给出的值。
哈夫曼编码
上面的信息都是独立同分布,在等概率的情况下的求得的$L_{n}$,再看看非等概率的情况下的优化情况。
举个例子:
我们假定有32条信息,每条信息出现的概率分别为1/2、1/4、1/8、1/16……依次递减,最后31、32两个信息出现的概率是1/2^31^、1/2^31^(这样32个信息的出现概率加起来就是1了)。现在需要用二进制数对它们进行编码。等长度和不等长度两种编码方法,我们来对比一下:
方法一:采用等长度编码,码长为5。因为是log32=5比特。
方法二:不等长度编码,如果出现概率高就短一些,概率低就长一些。 我们把第一条信息用0编码,第二条用10编码,第三条用110编码……最后31、32两条出现概率相同,都很低,码长都是31。第31条信息就用1111……110(30个1加1个0)编码,第32条信息,就用1111……111(31个1)来编码。 这样的编码虽然大部分码的长度都超过了5,但是乘以出现概率后,平均码长只有2。
也就是说方法二节省了60%的码长。如果利用这个原理进行数据压缩,可以在不损失任何信息的情况下压缩掉60%。
事实上,这种最短编码方法等于香农第一定律的继续,它最早是由MIT的教授哈夫曼发明的,因此也被称为“哈夫曼编码”。
在现实生活中,很多信息的组合,比单独一条信息,其概率分布差异更大,因此对它们使用哈夫曼编码进行信息压缩,压缩比会更高。
比如说,在汉语中,如果对汉字的频率进行统计,然后压缩,一篇文章通常能压缩掉50%以上,但是如果按照词进行频率统计,再用哈夫曼编码压缩,可以压缩掉70%以上。
其它编码
音频信号利用傅立叶变换将信息编码压缩,当然这样可能会有很少的信息损失。
图像信号利用离散余弦变换(DCT)结合图片基本模板来编码压缩,也可能会有很少的信息损失。
互信息
互信息的公式: \(I(X,Y)=\sum_{x \in X} \sum_{y \in Y} p(x, y) \log _{2} \frac{p(x, y)}{p(x) p(y)}\)
表示两个变量X与Y是否有关系,以及关系的强弱。
互信息是衡量相关程度的指标,相关不等于因果,世界上大多数联系都是相关联系,而非因果联系。
相关的联系可以强,可以弱,但弱相关其实没有什么意义,我们需要寻找和利用的是强相关性 。
联合熵
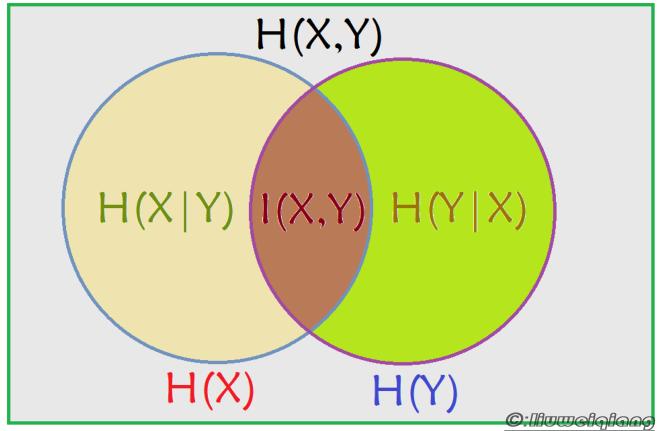
从上图可以看出,
互信息可以用熵减条件熵得出:
\[I(X,Y) = H(X) - H(X \vert Y)\]条件熵可以通过联合熵 - 熵 $H(X \vert Y) = H(X, Y) - H(Y)$ 表示,也可以通过熵 - 互信息$H(X \vert Y) = H(X) - I(X,Y)$表示。
交叉熵
其用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
\[交叉熵的公式为:\sum_{k=1}^{N} p_{k} \log _{2} \frac{1}{q_{k}}\]其中 $p_{k}$ 表示真实分布, $q_{k}$表示非真实分布。
举例子:
真实分布 $p_{k}=\left(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{8}\right)$, 非真实分布 $q_{k}=\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$,交叉熵为 $\frac{1}{2} * \log _{2} 4+\frac{1}{4} * \log _{2} 4+\frac{1}{8} * \log _{2} 4+\frac{1}{8} * \log _{2} 4=2$。
因此,交叉熵越低,这个策略就越好,最低的交叉熵也就是使用了真实分布所计算出来的信息熵,因为此时 $p_{k} = q_{k}$,交叉熵 = 信息熵。这也是为什么在机器学习中的分类算法中,我们总是最小化交叉熵,因为交叉熵越低,就证明由算法所产生的策略最接近最优策略,也间接证明我们算法所算出的非真实分布越接近真实分布。
当预测的 $q_{k}$和真实的$p_{k}$一致时,此时交叉熵就等于信息熵。
相对熵
相对熵,是用来衡量两个取值为正的函数或概率分布之间的差异。
假设我们想知道某个策略和最优策略之间的差异,我们就可以用相对熵来衡量这两者之间的差异,
即:
相对熵 = 某个策略的交叉熵 - 信息熵(根据系统真实分布计算而得的信息熵,为最优策略),公式如下,
\[\mathrm{KL}(\mathrm{p} \| \mathrm{q})=\mathrm{H}(\mathrm{p}, \mathrm{q})-\mathrm{H}(\mathrm{p})= \\ \sum_{k=1}^{N} p_{k} \log _{2} \frac{1}{q_{k}}-\sum_{k=1}^{N} p_{k} \log _{2} \frac{1}{p_{k}}=\sum_{k=1}^{N} p_{k} \log _{2} \frac{p_{k}}{q_{k}}\]当预测的 $q_{k}$和真实的$p_{k}$一致时,因为此时交叉熵就等于信息熵,相对熵计算出来也是等于0。
信息传播
香农第二定律
\[C=B \log _{2}\left(1+\frac{S}{N}\right)\]上面公式中,$C$为信道容量,$B$为带宽,$\frac{S}{N}$为信噪比。
通俗解释:
- 信息通道的传输率R,是无论如何无法超越信道容量C的,即R≤C。
- 总能找到一种编码方式,使得传输率R无限接近信道容量C,同时保证传输不出任何错误。
- 如果谁要试图超越信道容量传输信息,不论你怎样编码,出错的概率都是100%。
这三句话概括了香农第二定律的大意。
纠错编码
为了使一种码具有检错或纠错能力,必须对原码字增加多余的码元,以扩大码字之间的差别,使一个码字在一定数目内的码元上发生错误时,不致错成另一个码字。
准确地说,即把原码字按某种规则变成有一定剩余度的码字,并使每个码字的码元间有一定的关系。关系的建立称为编码。
码字到达收端后,用编码时所用的规则去检验。如果没有错误,则原规则一定满足,否则就不满足。由此可以根据编码规则是否满足以判定有无错误。
当不能满足时,在可纠能力之内按一定的规则确定错误所在的位置,并予以纠正,纠错并恢复原码字的过程称为译码。
码元间的关系为线性时,称为线性码;否则称为非线性码。检错码与其他手段结合使用,可以纠错。
信息加密
加密的过程看成是这样的:
明文+密码=密文
在加密的过程中如果给定明文和密码,你一定能得到唯一的密文;但是对于破密的人来讲,这个过程的逆过程非常困难,也就是说给你最后的密文,你是无法倒推出明文和密码。
常用的加密算法非常多,比如AES,RSA,MD5,SHA1等。

