在直角坐标系中,或者说在自然基下:
证明:
(1)刚开始的时候我们就说过,按照规定,零向量的方向任意,那么和某一向量夹角也任意,所以如果$ a $或$ b $是零向量,那么没有必要计算它们的夹角。
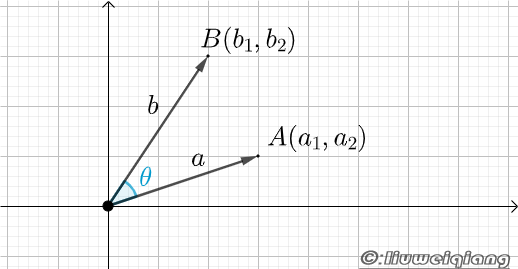
(2)根据欧氏几何中的余弦定理(对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍),我们可以得到:
\[AB^2=OA^2+OB^2-2OA\cdot OB\cos\theta\]上式可以通过向量来计算:
\[||\boldsymbol{a}-\boldsymbol{b}||^2=||\boldsymbol{a}||^2+||\boldsymbol{b}||^2-2||\boldsymbol{a}||||\boldsymbol{b}||\cos\theta,\quad (1)\]算一下(1)式的左边为多少,首先:
\[\begin{aligned} ||\boldsymbol{a_{}}-\boldsymbol{b_{}}|| &=||(a_1,a_2)-(b_1,b_2)||\\ \quad\\ &=||(a_1-b_1,a_2-b_2)||\\ \quad\\ &=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2} \end{aligned}\]取平方之后就得到(1)式的左边:
\[\begin{aligned} ||\boldsymbol{a_{}}-\boldsymbol{b_{}}||^2 &=(a_1-b_1)^2+(a_2-b_2)^2\\ \quad\\ &=\underbrace{(a_1^2+a_2^2)}_{||\boldsymbol{a}||^2}+\underbrace{(b_1^2+b_2^2)}_{||\boldsymbol{b}||^2}-2a_1b_1-2a_2b2 \\ &=||\boldsymbol{a}||^2+||\boldsymbol{b}||^2-2a_1b_1-2a_2b2 \end{aligned}\]所以(1)式可以改写为:
\[\begin{aligned} ||\boldsymbol{a_{}}-\boldsymbol{b_{}}||^2 &=||\boldsymbol{a}||^2+||\boldsymbol{b}||^2-2a_1b_1-2a_2b2\\ \quad\\ &=||\boldsymbol{a}||^2+||\boldsymbol{b}||^2-2||\boldsymbol{a}||||\boldsymbol{b}||\cos\theta \end{aligned}\]在$ a $和$ b $都不是零向量的条件下,整理之后可得:
\[\cos\theta=\displaystyle\frac{a_1b_1+a_2b_2}{||\boldsymbol{a_{}}||||\boldsymbol{b_{}}||}\]
