滤波器概念
数字滤波器:指输入,输出均为数字信号,通过一定运算关系改变输入信号所含频率成分的相对比例或者滤除某些成分的器件。
可以做以下几种分类:
- 经典滤波器:也叫选频滤波器,用于加性噪声。
- 现代滤波器:统计学角度来运算,用于乘法性噪声,卷积性噪声。
经典滤波器
\[X(n)=S(n)+U(n)\]上面公式中,$U(n)$叠加在$S(n)$信号上,并且两个占有不同的频带,可以通过一个线性系统将$U(n)$有效去除。
tips:频带重叠,经典滤波器就无能为力了
如果将一个脉冲信号输入到滤波器中,所得到的输出被称为滤波器的脉冲响应,FIR滤波器的脉冲响应就是滤波器的系数,而IIR滤波器的脉冲响应就不是很直观了。另外只要我们测量足够长的脉冲响应,就可以用FIR滤波器足够精确地模拟IIR滤波器。
经典滤波器按类型有两种:
-
有限脉冲响应(FIR)
-
无限脉冲响应(IIR)
按功能划分有几种:
- 低通(LP low pass)
- 高通(HP high pass)
- 带通(BP band pass)
- 带阻(BS band stop)
- 峰化(Peak)
- 低架(Low shelf)
- 高架(High shelf)
tips:高通,带通,带阻滤波器等可利用变量变换的方法,由低通滤波器变换得到。
IIR滤波器
典型模拟滤波器有:
- 巴特沃斯滤波器
- 切比雪夫滤波器
- 椭圆滤波器
根据传统的模拟滤波器来设计数字IIR滤波器,就是将模拟滤波器的传递函数做Z变换。
因此IIR滤波器的传输函数为:
\[H(z)=\frac{\sum_{r=0}^{M} b_{r} z^{r}}{1+\sum_{k=1}^{N} a_{k} z^{-k}}\]对应的差分方程为:
\[y(n)=\sum_{k=1}^{N} a_{k} y(n-k)+\sum_{k=0}^{M} b_{k} x(n-k)\]常用方程
模拟RC低通滤波:
\[\begin{array}{c} F_c = f_c/f_s ,f_{c}\, \text{is the cutoff frequency in Hertz}\\ b = e^{(-2 \pi F_c)} \\ a=1-b \\ y(n)=ax(n)+by(n-1) \end{array}\]模拟RC高通滤波:
\[\begin{array}{c} F_c = f_c/f_s ,f_{c}\, \text{is the cutoff frequency in Hertz}\\ c = e^{(-2 \pi F_c)} \\ b=-\frac{(1+c)}{2} \\ a=\frac{(1+c)}{2} \\ y(n)=ax(n)+bx(n-1)+cy(n-1) \end{array}\]二阶带通滤波:
\[\begin{array}{c} c = e^{(-2 \pi \frac{f_{bw}}{f_s})} ,f_{bw}\, \text{is the band width in Hertz} \\ b = -4c/(1+c)cos(2 \pi \frac{f_c}{f_s}) ,f_{c}\, \text{is the center frequency in Hertz}\\ a = (1-c)\sqrt{(1-\frac{b^2}{(4c)})} \\ y(n)= ax(n) - by(n-1) - cy(n-2) \end{array}\]双二阶滤波器:
关于IIR滤波器设计,可以通过这个博主的工具实时调节参数查看。
另外二次均衡器系数的设计公式,这里引用”Robert Bristow-Johnson“的研究成果,相关的滤波器公式可以跳转查看。结合scipy库,可以做出简单的均衡器,如下代码:
# -*- coding: utf-8 -*-
import scipy.signal as signal
import pylab as pl
import math
import numpy as np
def design_equalizer(freq, Q, gain, Fs):
'''设计二次均衡滤波器的系数'''
A = 10**(gain/40.0)
w0 = 2*math.pi*freq/Fs
alpha = math.sin(w0) / 2 / Q
b0 = 1 + alpha * A
b1 = -2*math.cos(w0)
b2 = 1 - alpha * A
a0 = 1 + alpha / A
a1 = -2*math.cos(w0)
a2 = 1 - alpha / A
return [b0/a0,b1/a0,b2/a0], [1.0, a1/a0, a2/a0]
pl.figure(figsize=(8,4))
for freq in [1000, 2000, 4000]:
for q in [0.5, 1.0]:
for p in [5, -5, -10]:
b,a = design_equalizer(freq, q, p, 44100)
w, h = signal.freqz(b, a)
pl.semilogx(w/np.pi*44100, 20*np.log10(np.abs(h)))
pl.xlim(100, 44100)
pl.xlabel(u"频率(Hz)")
pl.ylabel(u"振幅(dB)")
pl.subplots_adjust(bottom=0.15)
pl.show()
FIR滤波器
FIR滤波器的传输函数:
\[H(z)=\sum_{i=0}^{N-1} b i z^{-i}\]对应的差分方程为:
\[y(n)=\sum_{k=0}^{N-1} W_{k} x(n-k)\]因此FIR本质就是对N个采样数据执行加权和平均的处理,设计FIR滤波器就是选取合适的滤波器系数W,使滤波器达到设计的要求。
由于高通,带通,带阻滤波器可由低通滤波器变换得到,因此研究低通滤波器比较方便。
理想低通滤波器具有如下两个性质:
- 矩形的幅频特性
- 线性的相频特性
根据以上两个特性对函数做傅里叶逆变换,可以得到Sa函数:
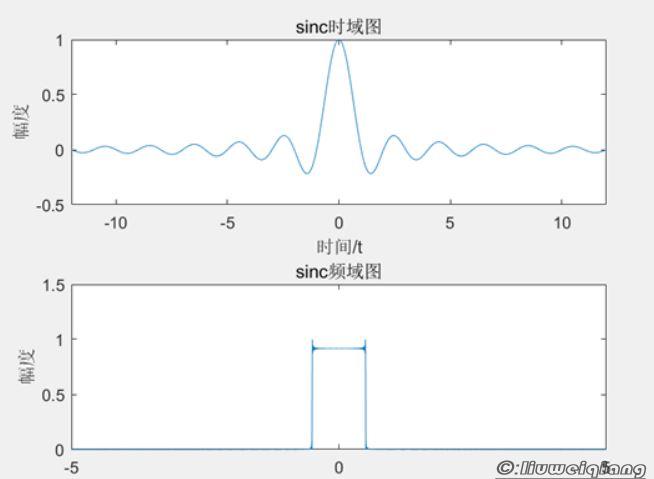
\[S_a(x) = \frac{sin(x)}{x}\]为了在信号与系统中便于使用,对Sa函数归一化处理,变成Sinc函数:
\[sinc(x)=\frac{sin(\pi x)}{\pi x}\]tips:Sinc函数之所以重要,是因为它的傅立叶变换正好是幅值为1的矩形脉冲。
Sinc滤波器近似一个只保留低频信号的理想低通滤波器,因为在频域它的形状近似一个矩形函数,如下图所示:
Sinc函数是个连续的函数,是个无限冲击响应系统,为了在离散系统中使用,还需要加窗处理。
窗函数
FIR滤波器要配合窗函数使用,目前主流的窗函数就那么几种:
- 矩形窗:FIR需要截断序列,因此默认就是使用矩形窗
- 三角形窗
- 汉宁窗(Hanning)
- 海明窗(Hamming)
- 布莱克曼窗(Blackman)
- 凯泽窗(Kaiser)
另外各个窗函数都有幅值恢复系数,如下图:

IIR&FIR关系
如果将一个脉冲信号输入到滤波器中,所得到的输出被称为滤波器的其脉冲响应。所谓脉冲信号就是在时刻0为1,其余时刻均为0的信号。根据FIR滤波器的公式,FIR滤波器的脉冲响应就是滤波器的系数。而IIR滤波器的脉冲响应就不是很直观了。
可以使用IIR滤波器,先计算脉冲信号响应,然后把脉冲信号响应当做FIR滤波器的系数,效果和IIR滤波器差不多,因此只要我们测量足够长的脉冲响应,就可以用FIR滤波器足够精确地模拟IIR滤波器。
演示代码如下:
# -*- coding: utf-8 -*-
import scipy.signal as signal
import numpy as np
import pylab as pl
# 某个均衡滤波器的参数
a = np.array([1.0, -1.947463016918843, 0.9555873701383931])
b = np.array([0.9833716591860479, -1.947463016918843, 0.9722157109523452])
# 44.1kHz, 1秒的频率扫描波
t = np.arange(0, 0.5, 1/44100.0)
x= signal.chirp(t, f0=10, t1 = 0.5, f1=1000.0)
y = signal.lfilter(b, a, x)
ns = range(10, 1100, 100)
err = []
for n in ns:
# 计算脉冲响应
impulse = np.zeros(n, dtype=np.float)
impulse[0] = 1
h = signal.lfilter(b, a, impulse)
# 直接FIR滤波器的输出
y2 = signal.lfilter(h, 1, x)
# 输出y和y2之间的误差
err.append(np.sum((y-y2)**2))
# 绘图
pl.figure(figsize=(8,4))
pl.semilogy(ns , err, "-o")
pl.xlabel(u"脉冲响应长度")
pl.ylabel(u"FIR模拟IIR的误差")
pl.show()
IIR&FIR对比
IIR滤波器使用反馈,而且往往是模仿传统的模拟滤波器的响应。反馈的用途意味着他们的脉冲响应是递归的,并延伸到无限的时段。虽然可以用比FIR滤波器更少的计算来实施IIR滤波器,但IIR滤波器可能有稳定性的问题。
相比之下, FIR滤波器没有反馈,这意味着它的脉冲响应在一个有限的时间范围之内,因此FIR滤波器稳定性优于IIR滤波器。
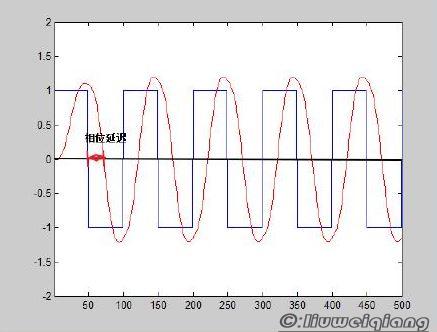
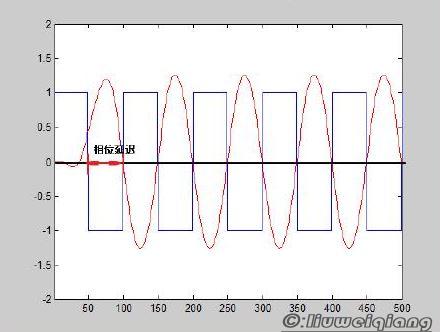
另外FIR具有严格的线性相位(FIR 为线性相位延迟,IIR 为非线性相位延迟),如下图所示:
上图为原始信号
上图为IIR滤波器后效果
上图为FIR滤波器后效果
综上对比,在考虑计算量的时候可以使用IIR滤波器,比如常用EQ调节,可以使用双二阶滤波器。如果算法使用到了FFT,可以结合使用FIR滤波器,灵活性非常高,可操作的空间大。
频率响应
无论IIR和FIR滤波器设计好后,可以通过python使用scipy.signal.freqz来计算,分析下该函数的计算方法:
def freqz(b, a=1, worN=512, whole=False, plot=None, fs=2*pi, include_nyquist=False):
b = atleast_1d(b)
a = atleast_1d(a)
if worN is None:
# For backwards compatibility
worN = 512
h = None
if _is_int_type(worN):
N = operator.index(worN)
del worN
if N < 0:
raise ValueError('worN must be nonnegative, got %s' % (N,))
lastpoint = 2 * pi if whole else pi
# if include_nyquist is true and whole is false, w should include end point
w = np.linspace(0, lastpoint, N, endpoint=include_nyquist and not whole)
if (a.size == 1 and N >= b.shape[0] and
sp_fft.next_fast_len(N) == N and
(b.ndim == 1 or (b.shape[-1] == 1))):
# if N is fast, 2 * N will be fast, too, so no need to check
n_fft = N if whole else N * 2
if np.isrealobj(b) and np.isrealobj(a):
fft_func = sp_fft.rfft
else:
fft_func = sp_fft.fft
h = fft_func(b, n=n_fft, axis=0)[:N]
h /= a
if fft_func is sp_fft.rfft and whole:
# exclude DC and maybe Nyquist (no need to use axis_reverse
# here because we can build reversal with the truncation)
stop = -1 if n_fft % 2 == 1 else -2
h_flip = slice(stop, 0, -1)
h = np.concatenate((h, h[h_flip].conj()))
if b.ndim > 1:
# Last axis of h has length 1, so drop it.
h = h[..., 0]
# Rotate the first axis of h to the end.
h = np.rollaxis(h, 0, h.ndim)
else:
w = atleast_1d(worN)
del worN
w = 2*pi*w/fs
if h is None: # still need to compute using freqs w
zm1 = exp(-1j * w)
h = (npp_polyval(zm1, b, tensor=False) /
npp_polyval(zm1, a, tensor=False))
w = w*fs/(2*pi)
if plot is not None:
plot(w, h)
return w, h
对于FIR滤波器,当长度比较长的时候是通过直接计算FFT来实现的,走下面的流程:
if (a.size == 1 and N >= b.shape[0] and
sp_fft.next_fast_len(N) == N and
(b.ndim == 1 or (b.shape[-1] == 1))):
对于IIR滤波器,其实就是4行代码实现:
w = np.linspace(0, lastpoint, N, endpoint=include_nyquist and not whole)
...
if h is None: # still need to compute using freqs w
zm1 = exp(-1j * w)
h = (npp_polyval(zm1, b, tensor=False) /
npp_polyval(zm1, a, tensor=False))
因为IIR滤波器的传输函数为: \(H(z)=\frac{\sum_{r=0}^{M} b_{r} z^{r}}{1+\sum_{k=1}^{N} a_{k} z^{-k}}\) 其中z为复数平面上的任意一点。当z为单位圆上的点(此时$\sigma$为0,复频域变成频域),即$z=e^{j \omega}$,$H(z)$就是滤波器的频率响应。$\omega$被称之为圆频率,当其取值从0到2*pi变化时,$e^{j \omega}$正好绕复数平面单位圆转一圈。由于复数平面上下两个半平面的复数存在共轭关系,因此通常只需要求上半圆的频率响应,因此下面的语句将上半圆等分为N份:
w = np.linspace(0, lastpoint, N, endpoint=include_nyquist and not whole)
然后计算w中每点对应的复数值$z^{-1}$,注意这里将负号带入,于是传递函数的分子分母部分就都变成了zm1的多项式函数:
zm1 = exp(-1j * w)
最后带入传递函数的公式中计算出频率响应h:
h = (npp_polyval(zm1, b, tensor=False) /
npp_polyval(zm1, a, tensor=False))
返回值w和h代表上述中的角频率和频率响应复数值:
Returns
-------
w : ndarray
The frequencies at which `h` was computed, in the same units as `fs`.
By default, `w` is normalized to the range [0, pi) (radians/sample).
h : ndarray
The frequency response, as complex numbers.
由于数组zm1中的值都为复数,因此所得到的频率响应h的值也都是复数。复数的幅值对应于频率响应中的增益特性,而其相角对应于频率响应中相位特性。
现代滤波器
乘法性噪声:
\[X(n)=S(n)U(n)\]卷积性噪声:
\[X(n)=S(n) * U(n)\]加行噪声(频带重叠):
\[X(n)=S(n)+U(n)\]信号的频谱和噪声谱混叠在一起,靠经典滤波器难以区分,因此一般用统计学的方法,从含有噪声的数据中估计出信号。
这类滤波器按种类划分:
- 维纳滤波器(Wiener filter)
- 卡尔曼滤波器(Kalman filter)
- 自适应滤波器(Adaptive filter)
- …
上面这些,尤以维纳滤波器作为代表,在语音噪声的去除算法中,就是用此种滤波器,配合贝叶斯估计,效果不错。