项目用到ADPCM编解码算法,在此做个记录,顺带理一理原理。
PCM
PCM(Pulse Code Modulation)脉冲编码调制是把声音从模拟信号转化为数字信号的技术,把一个时间连续取值连续的模拟信号变换成时间离散取值离散的数字信号,模拟信号转化为数字信号需要三个步骤:采样、量化、编码。
PCM约定俗成为无损编码,因为PCM代表了数字音频中最佳的保真水准,并不意味着PCM就能够确保信号绝对保真,PCM也只能做到最大程度的无限接近。
DPCM
DPCM(Differential Pulse Code Modulation),差分脉冲编码调
PCM是不压缩的,通常数据量比较大,考虑到一般音频信息都是比较连续的,不会突然很高或者突然很低,两点之间差值不会太大,所以这个差值只需要很少的几个位(对于16bits精度的音频来考虑,比如4bit)即可表示,这样压缩比大约4:1。
举个例子(网上借鉴资料):
比如以下的简单递增8bits PCM序列。
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127}
如果直接传输或者存储该序列,则需要128 * 8bits = 1024bits。
但是仔细观察了这个序列就可以得知,每个序列之间的变化只有一个1,所以可以将初始值设定为满幅度的1/2(64),之后每次传输sample之间的增量1。这样立即得到了8:1的压缩比。
只需传输以下数据序列(以byte流表示,第一个sample为初始值,这里为64):
{ 00, 00, 00, 00, FF, FF, FF, FF, FF, FF, FF, FF, FF, FF, FF, FF}
在解码的时候,遇到bit=0则减,遇到bit=1则增加即可基本完全还原原始数据,如下:
红为解码结果,蓝色为原始信号

上面的例子是完全均等递增的例子,那么其他数据怎么办?考虑这样一个方波序列:
{127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 127, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
还是以上面的算法进行编码,结果为这样:
{ FF, FF, 00, 00, FF, FF, 00, 00, FF, FF, 00, 00, FF, FF, 00, 00}
进行解码之后,与原始波形相比是这样:
红为解码结果,蓝色为原始信号

DPCM对快速变化的信号响应不够快,这是因为DPCM使用1bit表示每两个sample之间的变化,故此变化的步长也就固定了。步长若设定的太大则会失调震荡,若设定的过小则无法响应快速变化,所幸的是,音频信号尤其是语音信号,变化幅度不可能有上述的方波那么夸张。
再来考虑一个正弦序列的实验结果:
红为解码结果,蓝色为原始信号

再来考虑一个直流序列的实验结果:
红为解码结果,蓝色为原始信号

CVSD
此种算法是针对DPCM的固定步长的改良,即遇到连续的1或者0则相应的修改步长。
一般情况下连续的门限为4或者3,还是针对上面的几种波形做实验:
红为解码结果,蓝色为原始信号




不难看出来,CVSD与DPCM相比起来对原始信号的还原度有所提高,但还原度还是不够。
ADPCM
DPCM使用固定步长,CVSD线性地调整步长,而ADPCM则是自适应地调整步长。
- 利用自适应的思想改变量化阶的大小,即使用小的量化阶(step size)去编码小的差值,使用大的量化阶去编码大的差值。
- 使用过去的样本值估算下一个输入样本的预测值,使实际样本值和预测值之间的差值总是最小。
编码原理图如下:
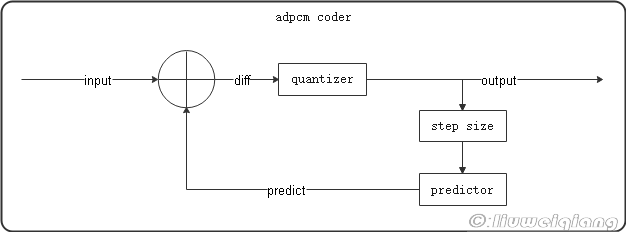
解码原理图如下:
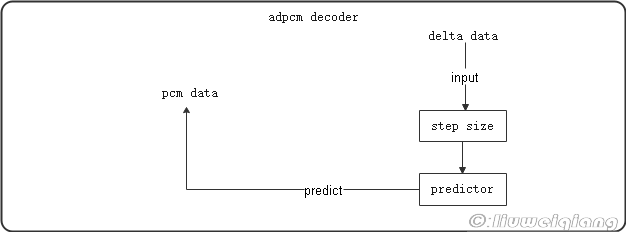
核心关键就是step size的自适应调整,另外由此可见原先的pcm数据和预测的数据还是会有点误差,毕竟adpcm属于有损压缩。
根据IMA Compatability Project的实现,参考以下16K采样率,16bits的代码:
struct adpcm_state {
short valprev;
char index;
};
void adpcm_init_state(struct adpcm_state *state);
int adpcm_coder_24k(const short [], char [], int, struct adpcm_state *);
int adpcm_decoder_24k(char [], short [], int, struct adpcm_state *);
int adpcm_decoder_24k_fill_zero(
unsigned char indata[],
unsigned char *enddata,
short outdata[],
int len,
struct adpcm_state *state);
/* Intel ADPCM step variation table */
static const int indexTable[4] = {
-1, -1, 2, 4,
};
static const int stepsizeTable[89] = {
7, 8, 9, 10, 11, 12, 13, 14, 16, 17,
19, 21, 23, 25, 28, 31, 34, 37, 41, 45,
50, 55, 60, 66, 73, 80, 88, 97, 107, 118,
130, 143, 157, 173, 190, 209, 230, 253, 279, 307,
337, 371, 408, 449, 494, 544, 598, 658, 724, 796,
876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066,
2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358,
5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899,
15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767
};
void
adpcm_init_state(struct adpcm_state *state)
{
state->valprev = 0;
state->index = 0;
}
int
adpcm_coder_24k(
const short indata[],
char outdata[],
int len,
struct adpcm_state *state)
{
int val; /* Current input sample value */
int sign; /* Current adpcm sign bit */
int delta; /* Current adpcm output value */
int diff; /* Difference between val and valprev */
int step; /* Stepsize */
int valpred; /* Predicted output value */
int vpdiff; /* Current change to valpred */
int index; /* Current step change index */
int i, k, r;
valpred = state->valprev;
index = state->index;
step = stepsizeTable[index];
k = r = 0;
for(i=0;i<len;i++){
val = indata[i];
/* Step 1 - compute difference with previous value */
diff = val - valpred;
sign = (diff < 0) ? 1 : 0;
if ( sign ) diff = (-diff);
/* Step 2 - Divide and clamp */
/* Note:
** This code *approximately* computes:
** delta = diff*4/step;
** vpdiff = (delta+0.5)*step/4;
** but in shift step bits are dropped. The net result of this is
** that even if you have fast mul/div hardware you cannot put it to
** good use since the fixup would be too expensive.
*/
delta = 0;
vpdiff = step >> 2;
if ( diff >= step ) {
delta |= 2;
diff -= step;
vpdiff += step;
}
step >>= 1;
if ( diff >= step ) {
delta |= 1;
vpdiff += step;
}
/* Step 3 - Update previous value */
if ( sign )
valpred -= vpdiff;
else
valpred += vpdiff;
/* Step 4 - Clamp previous value to 16 bits */
if ( valpred > 32767 )
valpred = 32767;
else if ( valpred < -32768 )
valpred = -32768;
/* Step 5 - Assemble value, update index and step values */
index += indexTable[delta];
if ( index < 0 ) index = 0;
if ( index > 88 ) index = 88;
step = stepsizeTable[index];
/* Step 6 - Output value */
outdata[k] = (outdata[k] << 1) | sign;
r++;
if(r == 8){
k++;
r = 0;
}
outdata[k] = (outdata[k] << 1) | (delta >> 1);
r++;
if(r == 8){
k++;
r = 0;
}
outdata[k] = (outdata[k] << 1) | (delta & 0x01);
r++;
if(r == 8){
k++;
r = 0;
}
}
/* Output last step, if needed */
while(r > 0){
outdata[k] <<= 1;
r++;
if(r == 8){
k++;
r = 0;
}
}
state->valprev = valpred;
state->index = index;
return k;
}
int
adpcm_decoder_24k(
char indata[],
short outdata[],
int len,
struct adpcm_state *state)
{
int sign; /* Current adpcm sign bit */
int delta; /* Current adpcm output value */
int step; /* Stepsize */
int valpred; /* Predicted value */
int vpdiff; /* Current change to valpred */
int index; /* Current step change index */
int i, k, r;
valpred = state->valprev;
index = state->index;
step = stepsizeTable[index];
k = 0;
r = 7;
for(i=0;i<len;i++){
/* Step 1 - get the sign & delta value */
sign = (indata[k] >> r) & 0x01;
r--;
if(r < 0){
k++;
r = 7;
}
delta = ((indata[k] >> r) & 0x01);
r--;
if(r < 0){
k++;
r = 7;
}
delta = (delta << 1) | ((indata[k] >> r) & 0x01);
r--;
if(r < 0){
k++;
r = 7;
}
/* Step 2 - Find new index value (for later) */
index += indexTable[delta];
if ( index < 0 ) index = 0;
if ( index > 88 ) index = 88;
/* Step 3 - Compute difference and new predicted value */
/*
** Computes 'vpdiff = (delta+0.5)*step/4', but see comment
** in adpcm_coder.
*/
vpdiff = step >> 2;
if ( delta & 2 ) vpdiff += step;
if ( delta & 1 ) vpdiff += step>>1;
if ( sign )
valpred -= vpdiff;
else
valpred += vpdiff;
#ifdef MODIFY_FIX_PLAY_VOL
valpred = valpred * FIX_PLAY_VOL_VAL_S30198SR + 0.5;
#endif
// amt_yp_scan(1);
/* Step 5 - clamp output value */
if ( valpred > 32767 )
valpred = 32767;
else if ( valpred < -32768 )
valpred = -32768;
/* Step 6 - Update step value */
step = stepsizeTable[index];
/* Step 7 - Output value */
outdata[i] = valpred;
}
if(r < 7)
k++;
state->valprev = valpred;
state->index = index;
return k;
}
其中:
static const int indexTable[4] = {
-1, -1, 2, 4,
};
里面的4代表,最大移动步长,代表预测值与真实值的逼近速度,前面-1,-1都是震荡调整步长。
另外:
static const int stepsizeTable[89] = {
7, 8, 9, 10, 11, 12, 13, 14, 16, 17,
19, 21, 23, 25, 28, 31, 34, 37, 41, 45,
50, 55, 60, 66, 73, 80, 88, 97, 107, 118,
130, 143, 157, 173, 190, 209, 230, 253, 279, 307,
337, 371, 408, 449, 494, 544, 598, 658, 724, 796,
876, 963, 1060, 1166, 1282, 1411, 1552, 1707, 1878, 2066,
2272, 2499, 2749, 3024, 3327, 3660, 4026, 4428, 4871, 5358,
5894, 6484, 7132, 7845, 8630, 9493, 10442, 11487, 12635, 13899,
15289, 16818, 18500, 20350, 22385, 24623, 27086, 29794, 32767
};
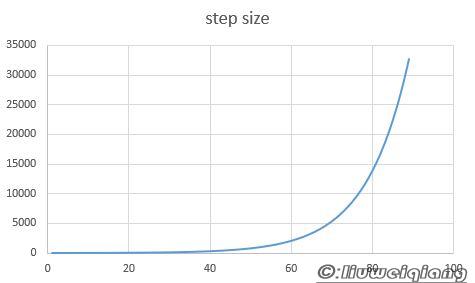
描点成图如下:
可以用如下公式来生成(和上述数据有一点点差异,但不影响):
\[y = Round(6.6833e^{0.0955x}),x=1,2,3,...,89\]将0-32767非线性划分为89段,作为量化的参考值,由此可见大部分的step size都是比较小的,当遇到突变的时候,step size也能快速反应过来,因此压缩还原度比较高。
该算法采用3bits来量化16bits,因此压缩率为16:3=5.3。
先看一个500个sample的编解码效果:
蓝色为原始数据,红色为编码解码还原数据,除了刚开始有点误差,后面看不出明显的误差。

上面IMA的ADPCM算法还有优化空间:
- 因为该算法是以len为长度来做压缩的,因此在len结尾处编码和解码都默认用0填充,造成一点点浪费,可以标记下,这样做还可以不用考虑编解码长度匹配的问题。目前这个算法如果编解码的长度不一致那就有问题了。
- 因为编码里面已经有解码过程,因此代码可以再精简紧凑些。
这些优化暂时不搞了,后面有时间再弄弄!