有时,我们需要对声音做变调处理,满足某种特定的使用场景,在此做个记录。
分类
目前变调算法从作用域来说分两种:
- 时域算法:优点是直接操作样本,无需重采样处理,计算量小,缺点是声音片段衔接处容易出现跳变,影响音频质量。
- 频域算法:优点是更精确的处理样本,缺点是计算量大。
时域算法
基本上分两步操作:
- 音频数据重采样
- 时域延拓或裁剪
音频数据重采样
音频重采样分为上采样和下采样:
-
下采样(抽取):新采样率 < 原采样率
-
上采样(插值):新采样率 > 原采样率
由数字信号处理中,时域信号和频域信号的时-频对偶特性可知:
- 时域的抽取,下采样,对应频域的延拓。
- 时域的插值,上采样,对应频域的压缩。
如果对信号的频率成分不做限制的话,频域的延拓可能会引发频谱混叠,频域的压缩可能会引发频谱镜像,因此,下采样之前,可能要经过滤波器滤波来防止混叠,即抗混叠滤波(anti-aliasing filter),上采样之后,可能也要经过滤波处理,即抗镜像滤波(anti-image filter)。
举例:
原始信号如下(Fs为采样率,Fm为信号的最大频率):

当Fs/2小于Fm,重叠部分就是频谱混叠:

在上采样后,因为会采样内插值算法,可能会因为不完美的滤波引入不需要的频谱镜像:
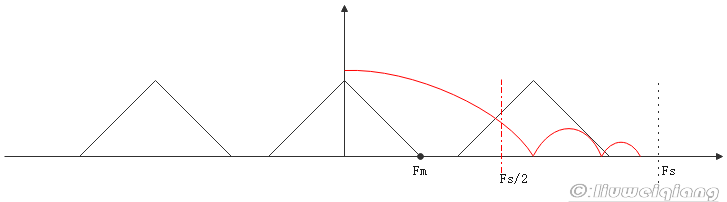
总结:下采样过程:低通->抽值 上采样过程:插值->低通
抽取算法
简单粗暴实现:
\[y(n)=x(M n) \quad n \geq 0 \quad M \geq 1\]因为是离散信号,M肯定是整数,因此成倍数的抽取,如果要完成采样率非倍数的变化,需要配合插值来完成。
插值算法
插值运算有多种算法,例如拉格朗日插值法、三次样条曲线、贝赛尔曲线、线性插值,等等。这些算法在图形学领域应用十分广泛,如对音频处理要求不高,也能适用于音频信号处理。
主流插值算法:
- 线性插值:当采样率远大于音频最高频率时可以使用,简单高效。
- 三次样条插值:当要求信号更平滑时,可以使用。
- 香农插值:配合kaiser窗函数使用,计算量比较大,基于香农理论设计,对音频损失最小。
tips:简单的理解插值,就是两个采样点之间先直接插入N个0值,但这势必会引入高频成分,因此一般选用低通滤波来平滑处理。
线性插值
\[h_{lin}[n] =\left\{\begin{array}{ll} 1-|n| / L, & |n| \leqslant L \\ 0, & \text { else } \end{array}\right.\]当L=5时,如下波形:
实际运用效果如下:
线性插值只用到内插的位置两旁的两个样本,就是把两个样本用直线连接后,该直线在对应内插位置上的的值就是所求的内插值。
实际运用中,对L归一化处理,离散数据中使用如下:
\[y(n')=(1-p)x(n)+px(n+1) \quad n \geq 0 \quad 1 \geq p \geq 0\]三次样条插值
\[h_{cu}[n] = \begin{cases} (a+2)|n / L|^{3}-(a+3)|n / L|^{2}+1, & 0 \leqslant|n| \leqslant L \\ a|n / L|^{3}-5 a|n / L|^{2}+8 a|n / L|-4 a, & L \leqslant|n| \leqslant 2 L \\ 0,& else \end{cases}\]当L=5,a=-0.5时,Cubic函数形状如下:
实际运用效果如下:
三次样条插值会用到内插位置两旁的四个样本,即左右各两个,曲线类似于对低通滤波器(sinc函数)进行截取后的曲线。
实际运用中,对L归一化处理,如下:
\[h_{cu}(x) = \left\{\begin{array}{ll} (a+2)|x|^{3}-(a+3)|x|^{2}+1, & 0 \leqslant|x| \leqslant 1 \\ a|x|^{3}-5 a|x|^{2}+8 a|x|-4 a, & 1 \leqslant|x| \leqslant 2 \\ 0, & e l s e \end{array}\right.\]离散数据中使用如下(C参数可调):
\[y(n')=(C_0p^3+C_1p^2+C_2p^1+C_3p^0)x(n) \\ +(C_4p^3+C_5p^2+C_6p^1+C_7p^0)x(n+1) \\ +(C_8p^3+C_9p^2+C_{10}p^1+C_{11}p^0)x(n+2) \\ +(C_{12}p^3+C_{13}p^2+C_{14}p^1+C_{15}p^0)x(n+3), \\ \quad n \geq 0 \quad 1 \geq p \geq 0\]香农插值
对于数字声音信号,我们关心的是插值运算的结果和原声音信号的误差。由香农定理可知,如果取样频率高于模拟信号的最高频率的两倍,就可以从取样后的数字信号精确地恢复原模拟信号。因此最理想的数字声音信号的插值算法就是基于此理论,从而精确地恢复原信号。得到原信号之后,只要再对其用新的取样频率进行取样,就可以实现重取样了。这种插值算法也被称为限频带插值(Bandlimited Interpolation) ,可以查看相关理论介绍。
假设对于连续时间信号x(t)进行取样之后得到一个数列x(nTs),这里的1表示连续时间,n是一个整数,而Ts是取样周期。假设信号x(t)的频带在-Fs/2和Fs/2之间,Fs是取样频率,即 Fs=1/Ts。
使用下面的公式可以将取样数列x(nTs)还原为原始的连续时间信号x(t): \(\begin{array}{l} x(t)=\sum_{n=-\infty}^{\infty} x\left(n T_{s}\right) h\left(t-n T_{s}\right) \\ h(t)=\operatorname{sinc}\left(F_{s} t\right)=\frac{\sin \left(\pi F_{s} t\right)}{\pi F_{s} t} \end{array}\) 分析一下此公式的含义。取样之后的数字信号可以看做原模拟信号与周期是Ts的脉冲信号的乘积。由于两个时域信号的乘积,等于它们的频域信号的卷积,因此取样之后信号的频域就是原信号频谱与周期脉冲信号的频谱的卷积。脉冲信号转换成频域之后仍然是脉冲,两个脉冲之间的间隔刚好是取样频率Fs。这样一来,频域卷积的结果就是原模拟信号的频谱在频率轴上不断地重复,就好像时域中的周期信号一样。
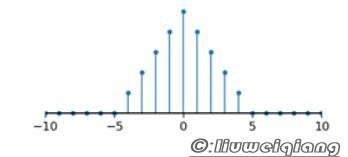
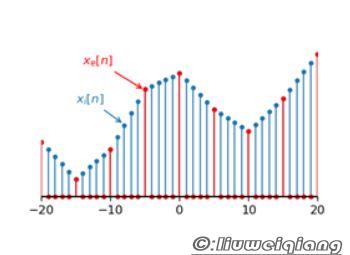
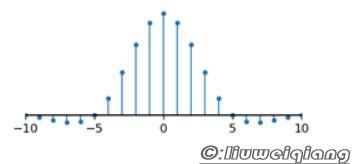
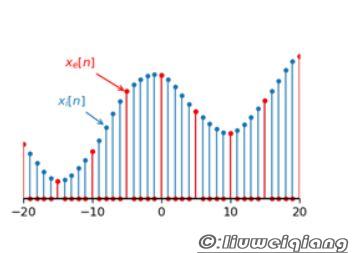
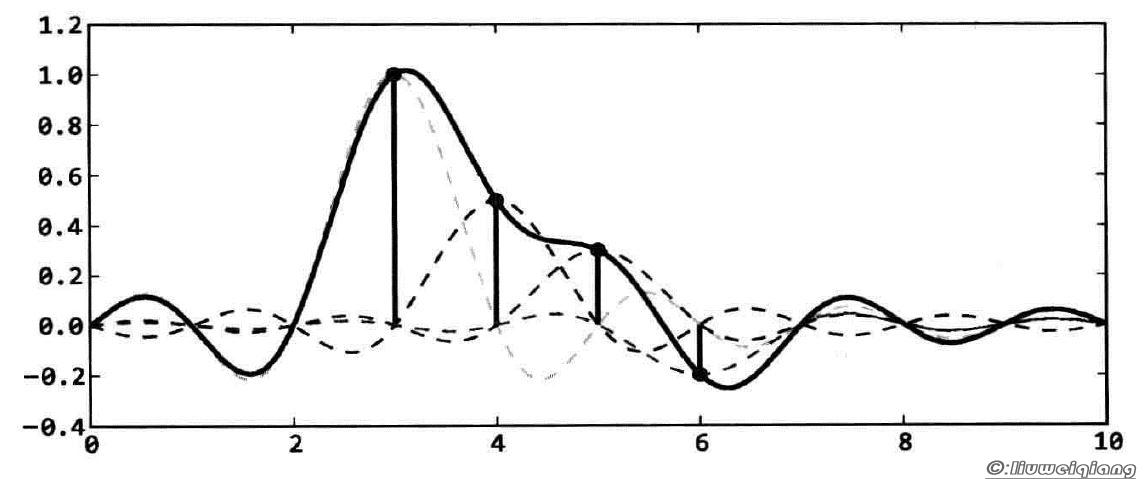
为了将取样后的信号还原为原模拟信号,需要对其进行低通滤波,如果使用通带为-Fs/2到Fs/2的理想低通滤波器,就可以精确地得到原信号的频谱。这种理想低通滤波器转换为时域波形,就是sinc函数。因此还原之后的模拟信号可以看做取样信号和sinc函数的卷积。或者可以理解为:在每个取样点处放置一个sinc函数波形,最终的模拟信号就是所有这些波形的叠加。如下图所示,数字信号的取样周期 为1,4个脉冲表示数字信号中的4个取样点,将其还原为模拟信号时,在每个取样点处放置一个用虚线表示的sinc函数波形,最后的模拟信号就是这4个波形的叠加,图中用粗实线表示。由于sinc函数波形在每个取样点处的值都为0,因此得到的模拟信号正好经过所有的取样点。
虽然理论上可以把取样后的信号还原为原信号,但是由于sinc函数波形是无限长的,实际计算中,只能取sinc函数波形的一部分进行卷积计算,并且需要使用窗函数加快收敛速度。
对比
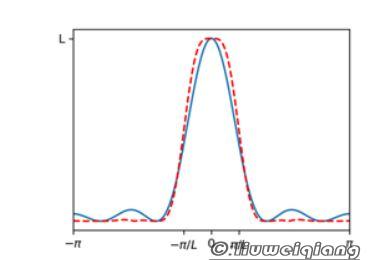
拿简单的来对比,观察线性插值和三次样条插值的频谱图如下:
上图蓝色实线为线性插值频谱,红色虚线为三次样条插值频谱。
对比线性插值以及三次样条插值,可以发现在 $ \omega<\frac{\pi}{L} $ 处,三次样条的旁瓣较宽,而在 $ \omega>\frac{\pi}{L} $ 处,三次样条的能量更小(幅度更低),即三次样条更接近于低通滤波器,因此三次样条插值会比线性插值的效果更好。
另外网上还有在线的其他SRC对比测试的工具,可以作为参考。
时域延拓或裁剪
典型的有SOLA、TDHS(Time-Domain Harmonic Sampling)、WSOLA和PSOLA几种,其中SOLA是最基本的,其它都是基于SOLA上的变种,下面主要介绍SOLA算法。
SOLA是Synchronous-OverLap-Add的简写,是将音频数据切断成几十到几百毫秒的片段,然后把这些片段按跳选或重复的原则来重新组成音频数据,其中,在片段的衔接处,由于音频数据的不连贯,会产生跳变,引入杂音,为了解决这个问题,可以采用加窗处理,并利用互相关函数,开辟一个搜索窗口动态寻找最匹配的衔接片段,以达到音频片段的平滑衔接。
如下图所示:

当然如果遇到多通道数据,比如立体声,环绕声,由于要保证所有通道的数据时间的一致性,只能使用多通道的互相关均值来选定一个合适的滑动窗口。
频域算法
频域处理虽然计算量大,但看起来也确实非常直观,如下图所示:

主要分三部分:
- FFT变换:将时域变换到频域。
- 拉伸频率:相位尽量不变,幅值改变。
- IFFT变换:将频域反变换到时域。
算法对比
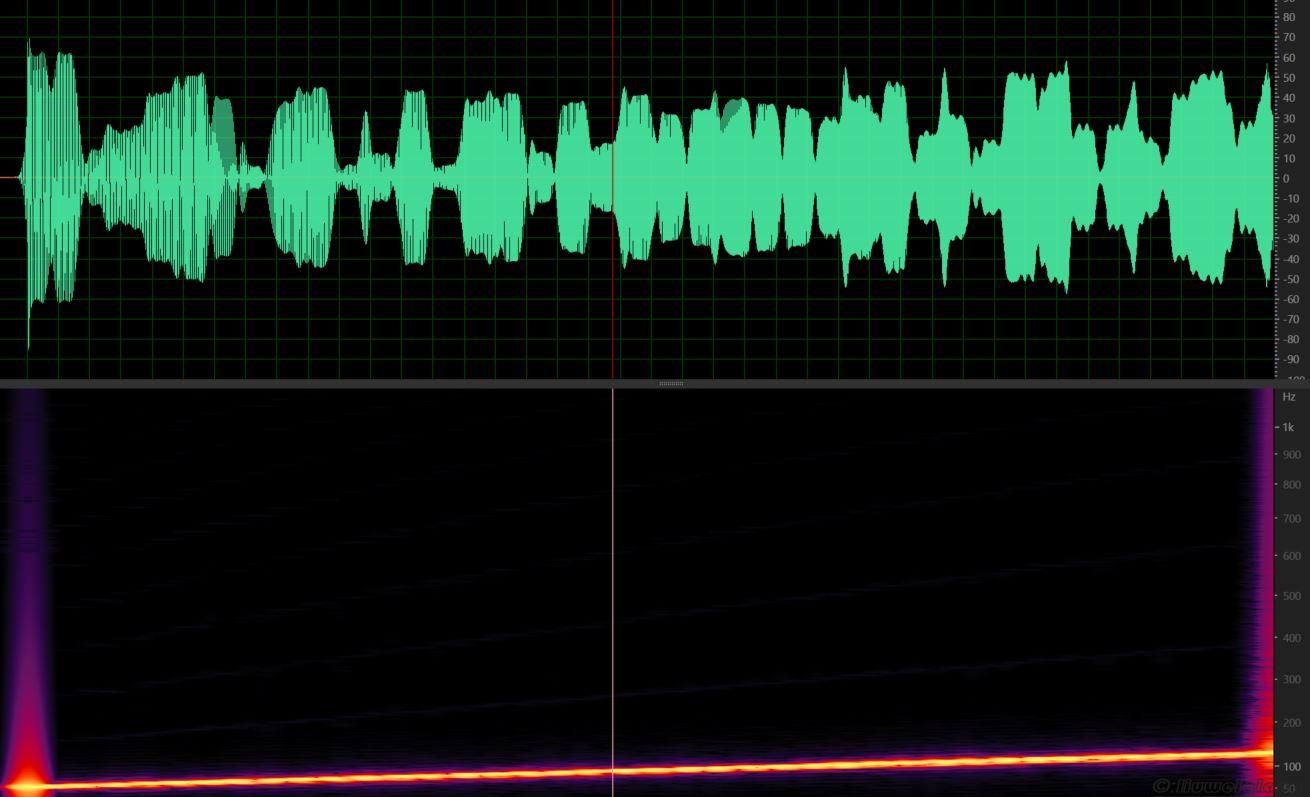
下图是采用时域算法将200hz信号升频的效果图,看频域很光滑,声音保持度比较不错。
下图是采用频域算法将100hz信号升频的效果图,采用“Short Time Fourier Transform” (STFT),为了达到靠近时域的精度,FFT的N比较大才行,虽然频率是比较光滑,但幅值包络不稳定,比较难控制。
总体来说还是倾向采用时域的算法处理,毕竟STFT经过加窗处理后,相位和包络很难调节。
网络资源
参考Free Resampling Software,里面有很多免费或者商业的重采样软件。