CRC 算法的数学基础
CRC 算法的数学基础就不再多啰嗦了,到处都是,简单提一下。它是以 GF(2) 多项式算术为数学基础的, GF(2) 多项式中只有一个变量 x ,其系数也只有 0 和 1 ,比如:
1 *x^6 + 0*x^5 + 1*x^4 + 0*x^3 + 0*x^2 +1*x^1 + 1*x^0
= x^6 + x^4 + x + 1
加减运算不考虑进位和退位。说白了就是下面的运算规则:
0 + 0 = 0 0 - 0 = 0
0 + 1 = 1 0 - 1 = 1
1 + 0 = 1 1 - 0 = 1
1 + 1 = 0 1 - 1 = 0
看看这个规则,其实就是一个异或运算。
每个生成多项式的系数只能是 0 或 1 ,因此我们可以把它转化为二进制形式表示, 比如 g(x)=x^4 + x + 1 ,那么 g(x) 对应的二进制形式就是 10011 , 于是我们就把 GF(2) 多项式的除法转换成了二进制形式,和普通除法没有区别,只是加减运算没有进位和退位。
比如基于上述规则计算 11010/1001 ,那么商是 11 ,余数就是 101 ,简单吧。
计算示例
设需要发送的信息为M = 1010001101,产生多项式对应的代码为P = 110101,R=5。在M后加5个0,然后对P做模2除法运算,得余数r(x)对应的代码:01110。故实际需要发送的数据是101000110101110。
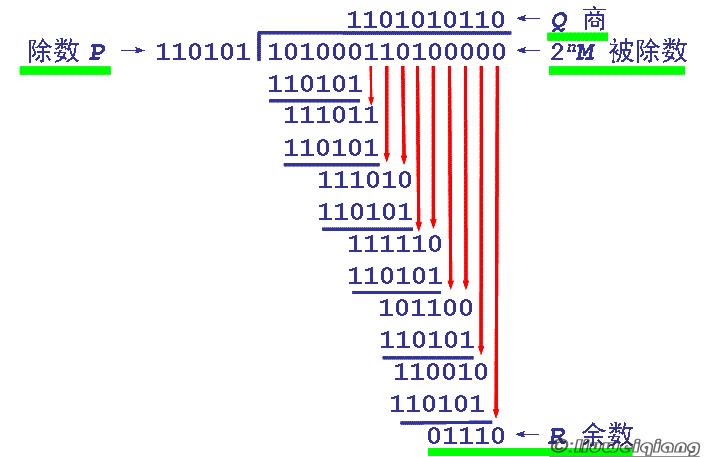
CRC 校验的基本过程
采用 CRC 校验时,发送方和接收方用同一个生成多项式 g(x) , g(x) 是一个 GF(2) 多项式,并且 g(x) 的首位和最后一位的系数必须为 1 。
CRC 的处理方法是:发送方用发送数据的二进制多项式 t(x) 除以 g(x) ,得到余数 y(x) 作为 CRC 校验码。校验时,以计算的校正结果是否为 0 为据,判断数据帧是否出错。设生成多项式是 r 阶的(最高位是 x^r )具体步骤如下面的描述。
发送方:
1 )在发送的 m 位数据的二进制多项式 t(x) 后添加 r 个 0 ,扩张到 m+ r 位,以容纳 r 位的校验码,追加 0 后的二进制多项式为 T(x) ;
2 )用 T(x) 除以生成多项式 g(x) ,得到 r 位的余数 y(x) ,它就是 CRC 校验码;
3 )把 y(x) 追加到 t(x) 后面,此时的数据 s(x) 就是包含了 CRC 校验码的待发送字符串;由于 s(x) = t(x) y(x) ,因此 s(x) 肯定能被 g(x) 除尽。
接收方:
1 )接收数据 n(x) ,这个 n(x) 就是包含了 CRC 校验码的 m+r 位数据;
2 )计算 n(x) 除以 g(x) ,如果余数为 0 则表示传输过程没有错误,否则表示有错误。从 n(x) 去掉尾部的 r 位数据,得到的就是原始数据。
数学推理
1.设欲传输的信息有K位,如图6.1所示
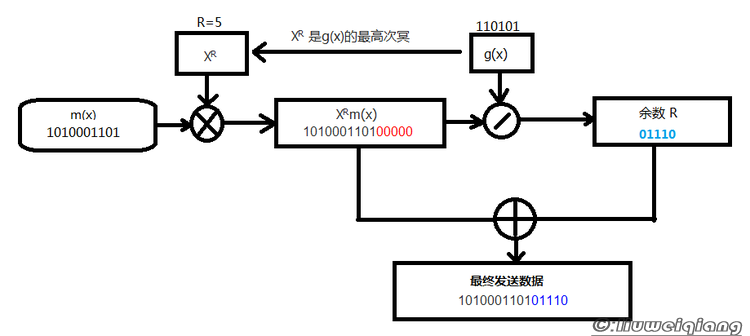
2.首先将欲传输的数据序列m(x)乘以 XR , 其中R为g(x)的最高次冥。
3.将得到的多项式XR m(x)除以约定的多项式g(x)
4.忽略除法结果的“商”,取出其余数,并与XRm(x)相加,形成K+R位的发送序列,即:m’(x) = XRm(x) +r(x)
常见CRC参数模型如下
CRC算法参数模型解释: NAME:参数模型名称。 WIDTH:宽度,即CRC比特数。 POLY:生成项的简写,以16进制表示。例如:CRC-32即是0x04C11DB7,忽略了最高位的”1”,即完整的生成项是0x104C11DB7。 INIT:这是算法开始时寄存器(crc)的初始化预置值,十六进制表示。 REFIN:待测数据的每个字节是否按位反转,True或False。 REFOUT:在计算后之后,异或输出之前,整个数据是否按位反转,True或False。 XOROUT:计算结果与此参数异或后得到最终的CRC值。
| CRC算法名称 | 多项式公式 | 宽度 | 多项式 | 初始值 | 结果异或值 | 输入值反转 | 输出值反转 |
|---|---|---|---|---|---|---|---|
| CRC-4/ITU | x4 + x + 1 | 4 | 03 | 00 | 00 | true | true |
| CRC-5/EPC | x4 + x3 + 1 | 5 | 09 | 09 | 00 | false | false |
| CRC-5/ITU | x5 + x4 + x2 + 1 | 5 | 15 | 00 | 00 | true | true |
| CRC-5/USB | x5 + x2 + 1 | 5 | 05 | 1F | 1F | true | true |
| CRC-6/ITU | x6 + x + 1 | 6 | 03 | 00 | 00 | true | true |
| CRC-7/MMC | x7 + x3 + 1 | 7 | 09 | 00 | 00 | false | false |
| CRC-8 | x8 + x2 + x + 1 | 8 | 07 | 00 | 00 | false | false |
| CRC-8/ITU | x8 + x2 + x + 1 | 8 | 07 | 00 | 55 | false | false |
| CRC-8/ROHC | x8 + x2 + x + 1 | 8 | 07 | FF | 00 | true | true |
| CRC-8/MAXIM | x8 + x5 + x4 + 1 | 8 | 31 | 00 | 00 | true | true |
| CRC-16/IBM | x6 + x5 + x2 + 1 | 16 | 8005 | 0000 | 0000 | true | true |
| CRC-16/MAXIM | x6 + x5 + x2 + 1 | 16 | 8005 | 0000 | FFFF | true | true |
| CRC-16/USB | x6 + x5 + x2 + 1 | 16 | 8005 | FFFF | FFFF | true | true |
| CRC-16/MODBUS | x6 + x5 + x2 + 1 | 16 | 8005 | FFFF | 0000 | true | true |
| CRC-16/CCITT | x6 + x2 + x5 + 1 | 16 | 1021 | 0000 | 0000 | true | true |
| CRC-16/CCITT-FALSE | x6 + x2 + x5 + 1 | 16 | 1021 | FFFF | 0000 | false | false |
| CRC-16/x5 | x6 + x2 + x5 + 1 | 16 | 1021 | FFFF | FFFF | true | true |
| CRC-16/XMODEM | x6 + x2 + x5 + 1 | 16 | 1021 | 0000 | 0000 | false | false |
| CRC-16/DNP | x6 + x3 + x2 + x1 + x0 + x8 + x6 + x5 + x2 + 1 | 16 | 3D65 | 0000 | FFFF | true | true |
| CRC-32 | x2 + x6 + x3 + x2 + x6 + x2 + x1 + x0 + x8 + x7 + x5 + x4 + x2 + x + 1 | 32 | 04C11DB7 | FFFFFFFF | FFFFFFFF | true | true |
| CRC-32/MPEG-2 | x32 + x6 + x3 + x2 + x6 + x2 + x1 + x0 + x8 + x7 + x5 + x4 + x2 + x + 1 | 32 | 04C11DB7 | FFFFFFFF | 00000000 | false | false |
原始的 CRC 校验算法
根据多项式除法,我们就可以得到原始的 CRC 校验算法。假设生成多项式 g(x) 是 r 阶的,原始数据存放在 data 中,长度为 len 个 bit , reg 是 r+1 位的变量。 以 CRC-4 为例,生成多项式 g(x)=x^4 + x + 1 ,对应了一个 5bits 的二进制数字 10011 ,那么 reg 就是 5 bits 。
reg[1] 表明 reg 的最低位, reg[r+1] 是 reg 的最高位。
通过反复的移位和进行除法,那么最终该寄存器中的值去掉最高一位就是我们所要求的余数。所以可以将上述步骤用下面的流程描述:
reg = 0;
data = data追加r个;
pos = 1;
while(pos <= len)
{
if(reg[r+1] == 1) // 表明reg可以除以g(x)
{
// 只关心余数,根据上面的算法规则可知就是XOR运算
reg = reg XOR g(x);
}
// 移出最高位,移入新数据
reg = (reg<<1) | (data[pos]);
pos++;
}
return reg; // reg中的后r位存储的就是余数
改进一小步——从 r+1 到 r
由于最后只需要 r 位的余数,所以我们可以尝试构造一个 r 位的 reg ,初值为 0 ,数据 data 依次移入 reg[1] ,同时把 reg[r] 移出 reg 。
根据上面的算法可以知道,只有当移出的数据为 1 时, reg 才和 g(x) 进行 XOR 运算;于是可以使用下面的算法:
reg = 0;
data = data追加r个;
pos = 1;
while(pos < len)
{
hi-bit = reg[r];
// 移出最高位,移入新数据
reg = (reg<<1) | (data[pos]);
if(hi-bit == 1) // 表明reg可以除以g(x)
{
reg = reg XOR g(x);
}
pos++;
}
return reg; // reg中存储的就是余数
这种算法简单,容易实现,对任意长度生成多项式的 G ( x )都适用,对应的 CRC-32 的实现就是:
// 以4 byte数据为例
#define POLY 0x04C11DB7L // CRC32生成多项式
unsigned int CRC32_1(unsigned int data)
{
unsigned char p[8];
memset(p, 0, sizeof(p));
memcpy(p, &data, 4);
unsigned int reg = 0, idx = 0;
for(int i = 0; i < 64; i++)
{
idx = i/8;
int hi = (reg>>31)&0x01; // 取得reg的最高位
// 把reg左移1bit,并移入新数据到reg0
reg = (reg<<1)| (p[idx]>>7);
if(hi) reg = reg^POLY; // hi=1就用reg除以g(x)
p[idx]<<=1;
}
return reg;
}
从 bit 扩张到 byte 的桥梁
但是如果发送的数据块很长的话,这种方法就不太适合了。它一次只能处理一个 bit 的数据,效率太低。考虑能不能每次处理一个 byte 的数据呢?事实上这也是当前的 CRC-32 实现采用的方法。
这一步骤是通往基于校验表方法的桥梁,让我们一步一步来分析上面逐 bit 的运算方式,我们把 reg 和 g(x) 都采用 bit 的方式表示如下:
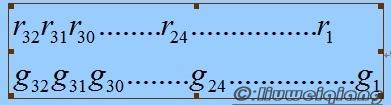
考虑把上面逐 bit 的算法执行 8 次,如果某次移出的不是 1 ,那么 reg 不会和 g(x) 执行 XOR 运算,事实上这相当于将 reg 和 0 执行了 XOR 运算。执行过程如下所示,根据 hi-bit 的值,这里的 G 可能是 g(x) 也可能是 0 。

从上面的执行过程清楚的看到,执行 8 次后, old-reg 的高 8bit 被完全移出, new-reg 就是 old-reg 的低 24bit 和数据 data 新移入的 8bit 和 G 一次次执行 XOR 运算所得到的。
XOR 运算满足结合律,那就是: A XOR B XOR C = A XOR (B XOR C) ,于是我们可以考虑把上面的运算分成两步进行:
1 )先执行 R 高 8bit 与 G 之间的 XOR 运算,将计算结果存入 X 中,如下面的过程所示。
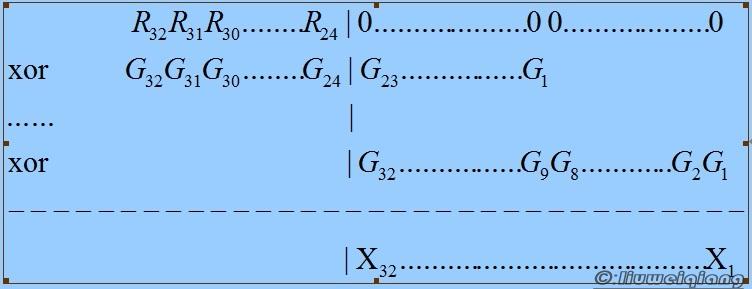
2 )将 R 左移 8bit ,并移入 8bit 的数据,得到的值就是 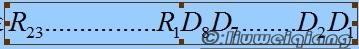 ,然后再与 X 做 XOR 运算。
,然后再与 X 做 XOR 运算。
根据 XOR 运算的结合率,最后的结果就等于上面逐 bit 的算法执行 8 次后的结果,根据这个分解,我们可以修改逐 bit 的方式,写出下面的算法。
// 以4 byte数据为例
#define POLY 0x04C11DB7L // CRC32生成多项式
unsigned int CRC32_2(unsigned int data)
{
unsigned char p[8];
memset(p, 0, sizeof(p));
memcpy(p, &data, 4);
unsigned int reg = 0, sum_poly = 0;
for(int i = 0; i < 8; i++)
{
// 计算步骤1
sum_poly = reg&0xFF000000;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x80000000; // 测试reg最高位
sum_poly <<= 1;
if(hi) sum_poly = sum_poly^POLY;
}
// 计算步骤2
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
}
return reg;
}
初见 Table-Driven
变换到上面的方法后,我们离 table-driven 的方法只有一步之遥了,我们知道一个字节能表示的正整数范围是 0~255 ,步骤 1 中的计算就是针对 reg 的高 Byte 位进行的,于是可以被提取出来,预先计算并存储到一个有 256 项的表中,于是下面的算法就出炉了,这个和上面的算法本质上并没有什么区别。
#define POLY 0x04C11DB7L // CRC32生成多项式
static unsigned int crc_table[256];
unsigned int get_sum_poly(unsigned char data)
{
unsigned int sum_poly = data;
sum_poly <<= 24;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x80000000; // 取得reg的最高位
sum_poly <<= 1;
if(hi) sum_poly = sum_poly^POLY;
}
return sum_poly;
}
void create_crc_table()
{
for(int i = 0; i < 256; i++)
{
crc_table[i] = get_sum_poly(i&0xFF);
}
}
// 以byte数据为例
unsigned int CRC32_3(unsigned int data)
{
unsigned char p[8];
memset(p, 0, sizeof(p));
memcpy(p, &data, 4);
unsigned int reg = 0, sum_poly = 0;
for(int i = 0; i < 8; i++)
{
// 计算步骤1
sum_poly = crc_table[(reg>>24)&0xFF];
// 计算步骤2
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
}
return reg;
}
更进一步
上面的这个算法已经是一个Table-Driven的CRC-32算法了,但是实际上我们看到的CRC校验代码都是如下的形式:
r=0;
while(len--)
r = (r<<8) ^ t[(r >> 24) ^ *p++];
下面我们将看看是做了什么转化而做到这一点的。
首先上述 CRC 算法中,我们需要为原始数据追加 r/8Byte 个 0 , CRC-32 就是 4Byte 。或者我们可以再计算原始数据之后,把 0 放在后面单独计算,像这样:
// 先计算原始数据
for(int i = 0; i < len; i++)
{
sum_poly = crc_table[(reg>>24)&0xFF];
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
}
// 再计算追加的4Byte 0
for(int i = 0; i < 4; i++)
{
reg = (reg<<8) ^ crc_table[(reg>>24)&0xFF];
}
这看起来已经足够好了,而事实上我们可以继续向下进行以免去为了附加的 0 而进行计算。在上面算法中,最后的 4 次循环是为了将输入数据的最后 r/8 位都移出 reg ,因为 0 对 reg 的值并没有丝毫影响。
对于 CRC-32 ,对于任何输入数据 Dn…D8…D5D4…D1 ,第一个 for 循环将 Dn…D8…D5 都依次移入,执行 XOR 运算再移出 reg ;并将 D4…D1 都移入了 reg ,但是并未移出;因此最后的 4 次循环是为了将 D4…D1 都移出 reg 。
Di 与 Ri 执行 XOR 运算后值将会更新,设更新后的值表示为 Di’ ,不论执行了多少次 XOR 运算。
如果 reg 初始值是 0 ,那么第一个 for 循环中开始的 4 次循环干的事情就是,把 Dn…Dn-3 移入到 reg 中(与 0 做 XOR 结果不变),执行 4 次后 reg 的值就是 Dn.Dn-1.Dn-2.Dn-3 ;
第 5 次循环的结果就是: reg = crc_table[Dn] ^ Dn-1.Dn-2.Dn-3.Dn-4 ;
第 6 次循环的结果就是: reg = crc_table[Dn-1’] ^ Dn-2’.Dn-3’.Dn-4 ; Dn 移出 reg 。
因此上面的计算可以分为 3 个阶段:
1 )前 4 次循环,将 Dn.Dn-1.Dn-2.Dn-3 装入 reg ;
2 )中间的 n-4 次循环,依次将 Di 移入 reg ,在随后的 4 次循环中,依次计算 Di+4 , Di+3 , Di+2 和 Di+1 对 Di 的影响;最后移出 reg ;
3 )最后的 4 次循环,实际上是为了计算 D4 , D3 , D2 和 D1 都能执行第 2 步的过程;
具体考察 Di :
1 ) Di 移入到 reg 中, R1=Di ,接着与 crc_table[R4] 执行 XOR 运算;
2 )循环 4 次后, Di 成为 reg 的最高位 R4 ,并且因为受到了 Dn…Di+1 的影响而更新为 Di’ ;
上面的运算步骤如下面所示,其中 F 是对应得 crc_table[R] 的值。
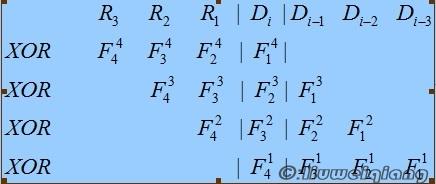
可以清晰的看到,最后 reg 的高 Byte 是 Di 和 F 之间一次次 XOR 运算的结果。依然根据 XOR 运算的结合律,我们可以分两步走:
1) 先执行 F 之间的 XOR 运算,设结果为 FF ,它就是 reg 的首字节;
2) 然后再直接将 Di 和 FF 进行 XOR 运算,并根据结果查 CRC 表;
3) 计算出 XOR 运算后, Di…Di-3 已经移入 reg ;因此再将查表结果和 (reg«8) 执行 XOR 运算即可;
这就是方法 2 ,于是我们的 table-driven 的 CRC-32 校验算法就可以写成如下的方式了:
reg = 0;
for(int i = 0; i < len; i++)
{
reg = (reg<<8) ^ crc_table[(reg>>24)&0xFF ^ p[i]];
}
郁闷的位逆转
看起来我们已经得到 CRC-32 算法的最终形式了,可是、可是在实际的应用中,数据传输时是低位先行的;对于一个字节 Byte 来讲,传输将是按照 b1,b2,…,b8 的顺序。而我们上面的算法是按照高位在前的约定,不管是 reg 还是 G(x) , g32,g31,…,g1 ; b8,b7,…,b1 ; r32,r31,…,r1 。
先来看看前面从 bit 转换到 Byte 一节中 for 循环的逻辑:
sum_poly = reg&0xFF000000;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x80000000; // 测试reg最高位
sum_poly <<= 1;
if(hi) sum_poly = sum_poly^POLY;
}
// 计算步骤2
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
在这里的计算中, p[i] 是按照 p8,p7,…,p1 的顺序;如果 p[i] 在这里变成了 p1,p2,…,p8 的顺序;那么 reg 也应该是 r1,r2,…,r32 的顺序,同样 G(x) 和 sum_poly 也要逆转顺序。转换后的 G(x) = POLY = 0xEDB88320 。
于是取 reg 的最高位的 sum_poly 的初值就从 sum_poly = reg & 0xFF000000 变成了 sum_poly = reg & 0xFF ,测试 reg 的最高位就从 sum_poly & 0x80000000 变成了 sum_poly&0x01 ;
移出最高位也就从 sum_poly«=1 变成了 sum_poly»=1 ;于是上面的代码就变成了如下的形式:
sum_poly = reg&0xFF;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x01; // 测试reg最高位
sum_poly >>= 1;
if(hi) sum_poly = sum_poly^POLY;
}
// 计算步骤2
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
为了清晰起见,给出完整的代码:
// 以4 byte数据为例
#define POLY 0xEDB88320L // CRC32生成多项式
unsigned int CRC32_2(unsigned int data)
{
unsigned char p[8];
memset(p, 0, sizeof(p));
memcpy(p, &data, 4);
unsigned int reg = 0, sum_poly = 0;
for(int i = 0; i < 8; i++)
{
// 计算步骤1
sum_poly = reg&0xFF;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x01; // 测试reg最高位
sum_poly >>= 1;
if(hi) sum_poly = sum_poly^POLY;
}
// 计算步骤2
reg = (reg<<8)|p[i];
reg = reg ^ sum_poly;
}
return reg;
}
依旧像上面的思路,把计算 sum_poly 的代码段提取出来,生成 256 个元素的 CRC 校验表,再修改追加 0 的逻辑,最终的代码版本就完成了,为了对比;后面给出了字节序逆转前的完整代码段。
// 字节逆转后的CRC32算法,字节序为b1,b2,…,b8
#define POLY 0xEDB88320L // CRC32生成多项式
static unsigned int crc_table[256];
unsigned int get_sum_poly(unsigned char data)
{
unsigned int sum_poly = data;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x01; // 取得reg的最高位
sum_poly >>= 1;
if(hi) sum_poly = sum_poly^POLY;
}
return sum_poly;
}
void create_crc_table()
{
for(int i = 0; i < 256; i++)
{
crc_table[i] = get_sum_poly(i&0xFF);
}
}
unsigned int CRC32_4(unsigned char* data, int len)
{
unsigned int reg = 0; // 0xFFFFFFFF,见后面解释
for(int i = 0; i < len; i++)
{
reg = (reg<<8) ^ crc_table[(reg&0xFF) ^ data[i]];
return reg;
}
}
// 最终生成的校验表将是:
// {0x00000000, 0x77073096, 0xEE0E612C, 0x990951BA,
// 0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3,
// … …}
// 字节逆转前的CRC32算法,字节序为b8,b7,…,b1
#define POLY 0x04C11DB7L // CRC32生成多项式
static unsigned int crc_table[256];
unsigned int get_sum_poly(unsigned char data)
{
unsigned int sum_poly = data;
sum_poly <<= 24;
for(int j = 0; j < 8; j++)
{
int hi = sum_poly&0x80000000; // 取得reg的最高位
sum_poly <<= 1;
if(hi) sum_poly = sum_poly^POLY;
}
return sum_poly;
}
void create_crc_table()
{
for(int i = 0; i < 256; i++)
{
crc_table[i] = get_sum_poly(i&0xFF);
}
}
unsigned int CRC32_4(unsigned char* data, int len)
{
unsigned int reg = 0;// 0xFFFFFFFF,见后面解释
for(int i = 0; i < len; i++)
{
reg = (reg<<8) ^ crc_table[(reg>>24)&0xFF ^ data[i]];
return reg;
}
}
长征结束了
到这里长征终于结束了, 事实上,还有最后的一小步,那就是 reg 初始值的问题,上面的算法中 reg 初始值为 0 。在一些传输协议中,发送端并不指出消息长度,而是采用结束标志,考虑下面的这几种可能的差错:
1 )在消息之前,增加 1 个或多个 0 字节;
2) 在消息 ( 包括校验码 ) 之后,增加 1 个或多个 0 字节;
显然,这几种差错都检测不出来,其原因就是如果 reg=0 ,处理 0 消息字节 ( 或位 ) , reg 的值保持不变。解决这种问题也很简单,只要使 reg 的初始值非 0 即可,一般取 0Xffffffff ,就像你在很多 CRC32 实现中发现的那样。
到这里终于可以松一口气了, CRC32 并不是像想象的那样容易的算法啊!事实上还真不容易!这就叫做“简单的前面是优雅,背后是复杂”!
